Byte and Bit Order Dissection【转】

Editors’ Note: This article has been updated since its original posting.

Software and hardware engineers who have to deal with byte and bit order issues know the process is like walking a maze. Though we usually come out of it, we consume a handful of our brain cells each time. This article tries to summarize the various areas in which the business of byte and bit order plays a role, including CPU, buses, devices and networking protocols. We dive into the details and hope to provide a good reference on this topic. The article also tries to suggest some guidelines and rules of thumb developed from practice.

We probably are familiar with the word endianness. First introduced by Danny Cohen in 1980, it describes the method a computer system uses to represent multi-byte integers.

Two types of endianness exist, big endian and little endian. Big endian refers to the method that stores the most significant byte of an integer at the lowest byte address. Little endian is the opposite; it refers to the method of storing the most significant byte of an integer at the highest byte address.

Bit order usually follows the same endianness as the byte order for a given computer system. That is, in a big endian system the most significant bit is stored at the lowest bit address; in a little endian system, the least significant bit is stored at the lowest bit address.

Every effort is made to avoid bit swapping in software when designing a system, because bit swapping is both expensive and tedious. Later sections describe how hardware takes care of it.

Just as most people write a number from left to right, the layout of a multi-byte integer should flow from left to right, that is, from the most significant to the least significant byte. This is the most clear way to write integers, as we can see in the following examples.

Here is how we would write the integer 0x0a0b0c0d for both big endian and little endian systems, according to the rule above:

Write Integer for Big Endian System

byte  addr       0         1       2        3
bit  offset  01234567 01234567 01234567 01234567
     binary  00001010 00001011 00001100 00001101
        hex     0a       0b      0c        0d

Write Integer for Little Endian System

byte  addr      3         2       1        0
bit  offset  76543210 76543210 76543210 76543210
     binary  00001010 00001011 00001100 00001101
        hex     0a       0b      0c        0d

In both cases above, we can read from left to right and the number is 0x0a0b0c0d.

If we do not follow the rule, we might write the number in the following way:

byte  addr      0         1       2        3
bit  offset  01234567 01234567 01234567 01234567
     binary  10110000 00110000 11010000 01010000

As you can see, it’s hard to make out what number we’re trying to represent.

Without losing generality, a simplified view of the computer system discussed in this article is drawn below.

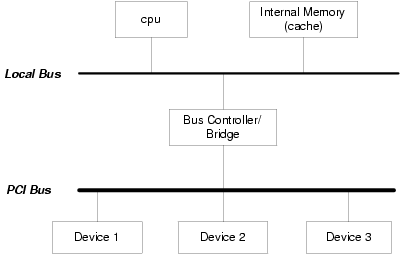
CPU, local bus and internal memory/cache all are considered to be CPU, because they usually share the same endianness. Discussion of bus endianness, however, covers only external bus. The CPU register width, memory word width and bus width are assumed to be 32 bits for this article.

The CPU endianness is the byte and bit order in which it interprets multi-byte integers from on-chip registers, local bus, in-line cache, memory and so on.

Little endian CPUs include Intel and DEC. Big endian CPUs include Motorola 680×0, Sun Sparc and IBM (e.g., PowerPC). MIPs and ARM can be configured either way.

The CPU endianness affects the CPU’s instruction set. Different GNU C toolchains for compiling the C code ought to be used for CPUs of different endianness. For example, mips-linux-gcc and mipsel-linux-gcc are used to compile MIPs code for big endian and little endian, respectively.

The CPU endianness also has an impact on software programs if we need to access part of a multi-byte integer. The following program illustrates that situation. If one accesses the whole 32-bit integer, the CPU endianness is invisible to software programs.

union {
    uint32_t my_int;
    uint8_t  my_bytes[4];
} endian_tester;
endian_tester et;
et.my_int = 0x0a0b0c0d;
if(et.my_bytes[0] == 0x0a )
    printf( "I'm on a big-endian systemn" );
else
    printf( "I'm on a little-endian systemn" );

The bus we refer to here is the external bus we showed in the figure above. We use PCI as an example below. The bus, as we know, is an intermediary component that interconnects CPUs, devices and various other components on the system. The endianness of bus is a standard for byte/bit order that bus protocol defines and with which other components comply.

Take an example of the PCI bus known as little endian. It implies the following: among the 32 address/data bus line AD [31:0], it expects a 32-bit device and connects its most significant data line to AD31 and least significant data line to AD0. A big endian bus protocol would be the opposite.

For a partial word device connected to bus, for example, an 8-bit device, little endian bus-like PCI specifies that the eight data lines of the device be connected to AD[7:0]. For a big endian bus protocol, it would be connected to AD[24:31].

In addition, for PCI bus the protocol requires each PCI device to implement a configuration space. This is a set of configuration registers that have the same byte order as the bus.

Just as all the devices need to follow bus’s rules regarding byte/bit endianness, so does the CPU. If a CPU operates in an endianness different from the bus, the bus controller/bridge usually is the place where the conversion is performed.

An alert reader nows ask this question, "so what happens if the endianness of the device is different from the endianness of the bus?" In this case, we need to do some extra work for communication to occur, which is covered in the next section.

Kevin’s Theory #1: When a multi-byte data unit travels across the boundary of two reverse endian systems, the conversion is made such that memory contiguousness to the unit is preserved.

We assume CPU and bus share the same endianness in the following discussion. If the endianness of a device is the same as that of CPU/bus, then no conversion is needed.

In the case of different endianness between the device and the CPU/bus, we offer two solutions here from a hardware wiring point of view. We assume CPU/bus is little endian and the device is big endian in the following discussion.

In this approach, we swap the entire 32-bit word of the device data line. We represent the data line of device as D[0:31], where D(0) stores the most significant bit, and bus line as AD[31:0]. This approach suggests wiring D(i) to AD(31-i), where i = 0, …, 31. Word Consistent means the semantic of the whole word is preserved.

To illustrate, the following code represents a 32-bit descriptor register in a big endian NIC card:

After applying the Word Consistent swap (wiring D[0:31] to AD[31:0]) , the result in the CPU/bus is:

Notice that it automatically is little endian for CPU/bus. No software byte or bit swapping is needed.

The above example is for those simple cases where data does not cross a 32-bit memory boundary. Now, let’s take a look at a case where it does. In the following code, vlan[0:24] has a value of 0xabcdef and crosses a 32-bit memory boundary.

After the Word Consistent swap, the result is:

Do you see what happened? The vlan field has been broken into two noncontiguous memory spaces: bytes[1:0] and byte(7). It violates Kevin’s Theory #1, and we are not able to define a nice C structure to access the in-contiguous vlan fields.

Therefore, the Word Consistent solution works only for data within word boundaries and does not work for data that may cross a word boundary. The second approach solves this problem for us.

In this approach, we do not swap bytes, but we do swap the bits within each byte lane (bit at device bit-offset i goes to bus bit-offset (7-i), where i=0…7) in hardware wiring. Byte Consistent means the semantic of the byte is preserved.

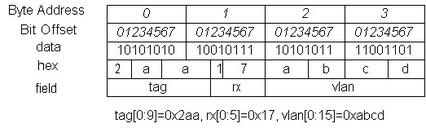
After applying this method, the big endian NIC device value in above results in this CPU/bus value:

Now, the three bytes of the vlan field are in contiguous memory space, and the content of each byte reads correctly. But this result still looks messy in byte order. However, because we now occupy a contiguous memory space, let the software do a byte swap for this 5-byte data structure. We get the following result:

We see that software byte swapping needs to be performed as the second procedure in this approach. Byte swapping is affordable in software, unlike bit swapping.

Kevin’s Theory #2: In a C structure that contains bit fields, if field A is defined in front of field B, then field A always occupies a lower bit address than field B.

Now that everything is sorted out nicely, we can define the C structure as the following to access the descriptor in the NIC:

struct nic_tag_reg {
        uint64_t vlan:24 __attribute__((packed));
        uint64_t rx  :6  __attribute__((packed));
        uint64_t tag :10 __attribute__((packed));
};

The endianness of network protocols defines the order in which the bits and bytes of an integer field of a network protocol header are sent and received. We also introduce a term called wire address here. A lower wire address bit or byte always is transmitted and received in front of a higher wire address bit or byte.

In fact, for network endianness, it is a little different than what we have seen so far. Another factor is in the picture: the bit transmission/reception order on the physical wire. Lower layer protocols, such as Ethernet, have specifications for bit transmission/reception order, and sometimes it can be the reverse of the upper layer protocol endianness. We look at this situation in our examples.

The endianness of NIC devices usually follow the endianness of the network protocols they support, so it could be different from the endianness of the CPU on the system. Most network protocols are big endian; here we take Ethernet and IP as examples.

Ethernet is big endian. This means the most significant byte of an integer field is placed at a lower wire byte address and transmitted/received in front of the least significant byte. For example, the protocol field with a value of 0x0806(ARP) in the Ethernet header has a wire layout like this:

wire byte offset:     0       1
hex             :    08      06

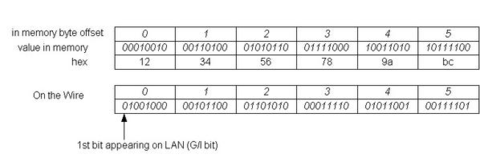
Notice that the MAC address field of the Ethernet header is considered as a string of characters, in which case the byte order does not matter. For example, a MAC address 12:34:56:78:9a:bc has a layout on the wire like that shown below, and byte 12 is transmitted first.

Bit Transmission/Reception Order

The bit transmission/reception order specifies how the bits within a byte are transmitted/received on the wire. For Ethernet, the order is from the least significant bit (lower wire address offset) to the most significant bit (higher wire address offset). This apparently is little endian. The byte order remains the same as big endian, as described in early section. Therefore, here we see the situation where the byte order and the bit transmission/reception order are the reverse.

The following is an illustration of Ethernet bit transmission/reception order:

We see from this that the group (multicast) bit, the least significant bit of the first byte, appeared as the first bit on the wire. Ethernet and 802.3 hardware behave consistently with the bit transmission/reception order above.

In this case, where the protocol byte order and the bit transmission/reception order are different, the NIC must convert the bit transmission/reception order from/to the host(CPU) bit order. By doing so, the upper layers do not have to worry about bit order and need only to sort out the byte order. In fact, this is another form of the Byte Consistent approach, where byte semantics are preserved when data travels across different endian domains.

The bit transmission/reception order generally is invisible to the CPU and software, but is important to hardware considerations such as the serdes (serializer/deserializer) of PHY and the wiring of NIC device data lines to the bus.

For either endianness, the Ethernet header can be parsed by software with the C structure below:

struct ethhdr
{
        unsigned char   h_dest[ETH_ALEN];       
        unsigned char   h_source[ETH_ALEN];     
        unsigned short  h_proto;                
};

The h_dest and h_source fields are byte arrays, so no conversion is needed. The h_proto field here is an integer, therefore a ntohs() is needed before the host accesses this field, and htons() is needed before the host fills up this field.

IP’s byte order also is big endian. The bit endianness of IP inherits that of the CPU, and the NIC takes care of converting it from/to the bit transmission/reception order on the wire.

For big endian hosts, IP header fields can be accessed directly. For little endian hosts, which are most PCs in the world (x86), byte swap needs to be be performed in software for the integer fields in the IP header.

Below is the structure of iphdr from the Linux kernel. We use ntohs() before reading integer fields and htons() before writing them. Essentially, these two functions do nothing for big endian hosts and perform byte swapping for little endian hosts.

struct iphdr {
#if defined(__LITTLE_ENDIAN_BITFIELD)
        __u8    ihl:4,
                version:4;
#elif defined (__BIG_ENDIAN_BITFIELD)
        __u8    version:4,
                ihl:4;
#else
#error  "Please fix <asm/byteorder.h>"
#endif
        __u8    tos;
        __u16   tot_len;
        __u16   id;
        __u16   frag_off;
        __u8    ttl;
        __u8    protocol;
        __u16   check;
        __u32   saddr;
        __u32   daddr;
        /*The options start here. */
};

Take a look at some interesting fields in the IP header:

version and ihl fields: According to IP standard, version is the most significant four bits of the first byte of an IP header. ihl is the least significant four bits of the first byte of the IP header.

There are two methods to access these fields. Method 1 directly extracts them from the data. If ver_ihl holds the first byte of the IP header, then (ver_ihl & 0x0f) gives the ihl field and (ver_ihl > > 4) gives the version field. This applies for hosts with either endianness.

Method 2 is to define the structure as above, then access these fields from the structure itself. In the above structure, if the host is little endian, then we define ihl before version; if the host is big endian, we define version before ihl. If we apply Kevin’s Theory #2 here that an earlier defined field always occupies a lower memory address, we find that the above definition in C structure fits the IP standard pretty well.

saddr and daddr fields: these two fields can be treated as either byte or integer arrays. If they are treated as byte arrays, there is no need to do endianness conversion. If they are treated as integers, then conversions need to be performed as needed. Below is a function with integer interpretation:

/*  dot2ip - convert a dotted decimal string into an 
 *           IP address 
 */
uint32_t dot2ip(char *pdot)
{
  uint32_t i,my_ip;
  my_ip=0;
  for (i=0; i<IP_ALEN; ++i) {
    my_ip = my_ip*256+atoi(pdot);
    if ((pdot = (char *) index(pdot, '.')) == NULL)
        break;             
        ++pdot;
    }
    return my_ip;
}

And here is the function with byte array interpretation:

uint32_t dot2ip2(char *pdot)
{
  int i;
  uint8_t ip[IP_ALEN];
  for (i=0; i<IP_ALEN; ++i) {
    ip[i] = atoi(pdot);
    if ((pdot = (char *) index(pdot, '.')) == NULL)
        break;          
     ++pdot;
  }
  return *((uint32_t *)ip);
}

The topic of byte and bit endianness can go even further than what we discussed here. Hopefully this article has covered the main aspects of it. See you next time in the maze.

Kevin Kaichuan He is a senior system software engineer at Solustek Corp. He currently is working on board bring-up, embedded Linux and networking stacks projects. His previous work experience includes being a software engineer at Cisco Systems and a research assistant in Computer Science at Purdue University. In his spare time, he enjoys digital photography, PS2 games and movies.